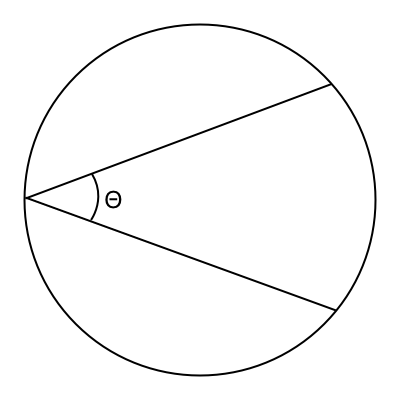
What angle would you cut a circle at to divide it into thirds?

The other day I was reading a tweet from Neil deGrasse Tyson, and it got me thinking… If you were going to cut a circle into three equal pieces using only two cuts, what would the angle to cut them be? (Θ in the diagram over on the right side there.) So I asked on Twitter, and eventually got a reply. This is my attempt to reconstruct the reasoning behind the answer.

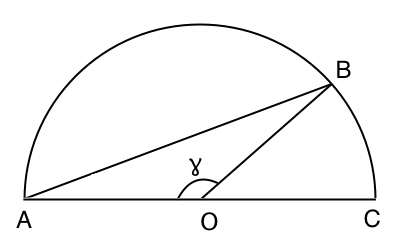The easiest way to figure this out, I believe, is to cut the circle in half, and then figure out what line divides the semicircle into a 2/3rds to 1/3rd ratio. So let’s do that, and label the points A, B, C, and O (for the origin), as shown on the left. We’ll also label the angle AOB as ɣ, because we'll be using it a little more later.

We know from this page that the area of a segment is r² × (ɣ - sin ɣ) / 2, and we want the segment formed by the line AB to contain 1/3rd of the total circle (or 1/3 × π × r²). Putting those together gives us the equation:
r² × (ɣ - sin ɣ) / 2 = π × r² / 3
multiplying both sides by 2, and diving both sides by r², we get
(ɣ - sin ɣ) = 2 × π / 3
Now all we have to do is simply solve for ɣ to get:
ɣ = 2.60533

That means that the angle BOC is π - ɣ, or 0.53626 radians (or 30.7º). Now, the inscribed angle is half the central angle, so in theory, to get the angle BAD, I should divide that by two, but then I’ll just need to multiply it by two again to account for the other half of the circle, so let’s skip all that, and just call it 30.7º.